[이산수학] 2.수학적 모델링

수학적 모델링?

이산수학을 배우면서 가장 처음 등장하는 말은 수학적 모델링이다. 수학적 모델링은 문제를 해결하기 위해 문제 영역을 수학적 구조에 매핑시켜서 보다 체계적으로 문제를 해결하는 방법론이다. 말이 너무 어렵다. 좀 더 이해하기 쉽게 생각해보자.

즉, 주어진 문제가 있을 때, 우리는 이 문제를 어떻게 풀 것인가에 대해서 고민할 것이다. 이 때 우리가 배웠던 수학적 개념(방정식, 함수) 등으로 문제의 구조를 바꿔 생각해서 문제 해결을 더 쉽게 하는 것이 바로 수학적 모델링의 핵심이다.

예를 한번 들어보자.

8명의 친구들이 중국집을 갔다.
3000원인 짜장면과 4000원인 짬뽕 둘 중 각자 먹고 싶은 것 하나씩 시켜 먹었다.
식사를 마치고 계산을 할 때 27000원이 나왔다.
그럼 이 친구들은 식당에서 짜장 몇 개 짬뽕 몇 개를 시켰는가?

위와 같은 예제는 아주 간단해서 똑똑한 사람들은 머릿속으로 쉽게 답을 낼 수 있을 것이다. 나는 이 문제가 복잡하다고 생각하기 때문에 내가 알고있는 방정식을 이용해보려고 한다.

x + y = 8
3000x + 4000y = 27000

이렇게 짜장면을 x 짬뽕을 y라는 변수로 지정하고 이를 방정식의 형태로 표현했다. 방정식을 풀어보면 짜장면 5개, 짬뽕 3개를 시켰다는 것을 알 수 있다.
이처럼 나는 문제를 해결하기 위해 문제를 방정식 이라는 수학적 구조에 문제를 매핑시켜 문제를 해결하였다. 문제를 수학적인 구조로 바꾸어 보다 문제 해결을 쉽게 하는 것. 이것이 수학적 모델링이라 할 수 있다.

다른 예시를 들어보자.

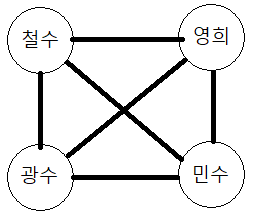
철수, 영희, 광수, 민수 네 사람이 파티에 갔다.
파티에서 네 사람이 서로 빠지지 않고 모두 악수를 할 때 악수는 총 몇 번 이뤄지는가?

위와 같은 현실 속의 문제를 해결하기 위해서 여러 방법을 사용할 수 있지만 나는 앞으로 배울 그래프를 이용하여 문제를 해결해 보려한다.

위의 그래프를 보면 각 정점을 선으로 이어 악수했음을 표현하였다. 선의 개수를 세어보면 총 6개이고 악수는 총 6번 이루어짐을 알 수 있다.
이번에는 문제를 그래프라는 수학적 구조에 매핑시켜 문제를 해결해보았다. 이와 같이 수학적 모델링을 통해서 복잡했던 문제를 간단하게 해결할 수 있다.

이산수학과 수학적 모델링

우리는 수학적 모델링에 대해서 알아보았다. 앞에서 보았듯이 수학적 모델링은 뭐 대단한 것이 아니다. 그저 우리가 알고있는 수학적인 개념을 문제에 도입하여 해결을 돕는 것이다. 우리는 문제를 해결하기 위해 수학을 도구로써 사용하는 것이다. 앞으로 이산수학을 통해 우리는 이 도구로 사용되는 수학적 개념에 대해서 배우게 될 것이다. 그렇다면 우리는 나중에 더 복잡한 문제가 다가왔을 때 다양한 도구를 가지고 있기 때문에 이를 효과적으로 해결할 수 있을 것이다.